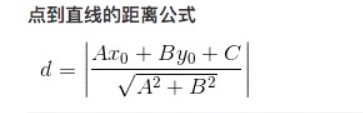2019-07-30-分类方法
1.主要内容
感知器模型
KNN 最近邻
决策树
贝叶斯分类器
SVM支持向量机
特征向量具有handcraft 以及CNN feature两种特征。
2.感知器模型
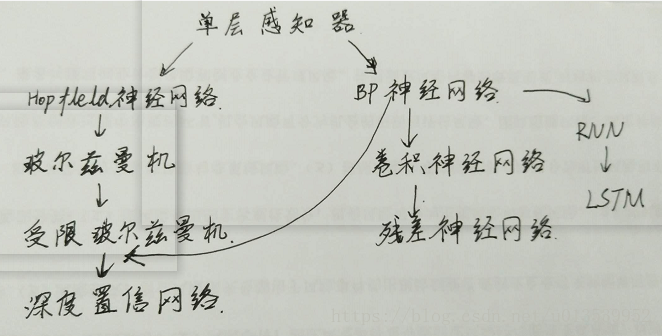
神经元超过阈值就被激活,有一个激活函数。发展历程:
人工神经网络的第一个里程碑是感知机perception, 这个名字其实有点误导, 因为它根本上是做决策的。 一个感知机其实是对神经元最基本概念的模拟 ,都未必有多少网络概念,他就是一个自动做决策的机器。比如说你要决定今天出不出去看电影, 你要考虑3个因素, 一个是女朋友在不在, 一个是电影好不好看, 另一个是今天有没有工作, 这三个因素每个人的权重都不同,有的人看重女朋友, 有的人看重工作,所以权重就不等, 最后每个人根据自己的权重做出0或1,去或不去, to be or not to be的决策。那么你怎么做呢? 你把三个要素按照它们需要的权重加和在一起, 在把这个分数送到一个叫sigmoid的门面前得到去或不去的决定, 工作原理如上图。比单层感知机更复杂的多层感知机-或者我们常说的深度网络, 是进行数据处理和模式识别的利器。 深度神经网络之所以能够处理这些数据类型,主要是因为这些数据本身具有的复杂结构很适合被CNN识别, 而人类不需要预先设计识别这些结构的函数而是任由网络学习, D-CNN 深度卷积网络能够同时看到一个图像从细节到抽象的结构,所以能够抓住一些我们人类都说不出的细节。
单层感知器由一个线性组合器和一个二值阈值元件组成。

输入向量为x,权重向量为w,w0为偏差。
简单的理解可以解释为:将x0,x1······xn的变量输入,经过组合器的整合,输出1或者-1,也就是通过组合器对输入变量判断其正确与否。
而这个判断的依据就是权重w0,w1······wn。
因为线性组合器是实现加法的方式,根据向量的运算法则,所以以上公式的输入值可以理解为: w0+x1w1+······+xnwn

单个数据的输入判断就是这样,下面我们将它扩展到多个数据,如下图所示:

在整个的感知器算法中,是有明确的数学公式,通过线性组合器的组装进行分类判断:

这就是详细的组合器算法。其中偏振因子b,一般会用w0表示,这时会加入一个偏振输入变量x0,不过x0恒等于1,也就是以上所描述的公式。
3.感知机代码
#!/usr/bin/env python
# -*- coding: UTF-8 -*-
import matplotlib.pyplot as plt
import numpy as np
from functools import reduce
#此函数的调用比较特殊,不需要参数,只是定义了公式
def add(x,y):
return x+y
class Perceptron():
'''
Desc:
感知器类
Args:
None
Returns:
None
'''
def __init__(self,input_num,activator):
'''
Desc:
初始化感知器
Args:
input_num —— 输入参数的个数
activator —— 激活函数
Returns:
None
'''
# 设置的激活函数
self.activator = activator
# 权重向量初始化为 0
self.weights = [0.0 for _ in range(input_num)]
# 偏置项初始化为 0
self.bias = 0.0
def __str__(self):
'''
Desc:
将感知器信息打印出来
Args:
None
Returns:
None
'''
return 'weights\t:%s\n b0ias\t:%f\n' % (self.weights, self.bias)
def predict(self,input_vec):
'''
Desc:
输入向量,输出感知器的计算结果
Args:
input_vec —— 输入向量
Returns:
感知器的计算结果
'''
# 将输入向量的计算结果返回
# 调用 激活函数 activator ,将输入向量输入,计算感知器的结果
# reduce() 函数是 python 2 的内置函数,从 python 3 开始移到了 functools 模块
# reduce() 从左到右对一个序列的项累计地应用有两个参数的函数,以此合并序列到一个单一值,
# 例如 reduce(lambda x,y: x+y, [1,2,3,4,5]) 计算的就是 ((((1+2)+3)+4)+5)
# map() 接收一个函数 f 和一个 list ,并通过把函数 f 依次作用在 list 的每个元素上,得到一个新的 list 返回。
# 比如我们的 f 函数是计算平方, map(f, [1,2,3,4,5]) ===> 返回 [1,4,9,16,25]
# zip() 接收任意多个(包括 0 个和 1个)序列作为参数,返回一个 tuple 列表。
# 例:x = [1,2,3] y = [4,5,6] z = [7,8,9] xyz = zip(x, y, z) ===> [(1,4,7), (2,5,8), (3,6,9)]
pack = zip(input_vec,self.weights) # 把输入向量和权重变成一个tuple
multi = []
for (x,w) in pack: # 对于每一对这个pack
multi.append(x*w)
activtion = reduce(add, multi) #累加起来
# 此处python3 lambda无法传入一个tuple的两个变量,因此将tuple当作一个整体,tp[0]为input_vec,tp[1]为self.weights
return self.activator(activtion + self.bias) #返回激活的那一个···值,可能是自带的?
#还有一种更加简洁明了的写法,很清楚明白
# return self.activator(sum([x*w for (x,w) in zip(input_vec,self.weights)])+self.bias)
def train(self,input_vecs,labels,iteration,rate):
'''
Desc:
输入训练数据:一组向量、与每个向量对应的 label; 以及训练轮数、学习率
Args:
input_vec —— 输入向量
labels —— 数据对应的标签
iteration —— 训练的迭代轮数
rate —— 学习率
Returns:
None
'''
for i in range(iteration):
self._one_iteration(input_vecs,labels,rate)
def _one_iteration(self,input_vecs,labels,rate):
'''
Desc:
训练过程的一次迭代过程
Args:
input_vecs —— 输入向量
labels —— 数据对应的标签
rate —— 学习率
Returns:
None
'''
# zip() 接收任意多个(包括 0 个和 1个)序列作为参数,返回一个 tuple 列表。
# 例:x = [1,2,3] y = [4,5,6] z = [7,8,9] xyz = zip(x, y, z) ===> [(1,4,7), (2,5,8), (3,6,9)]
samples = zip(input_vecs, labels)
# 对每个样本,按照感知器规则更新权重
for (input_vec, label) in samples:
# 计算感知器在当前权重下的输出
output = self.predict(input_vec)
# 更新权重
output = self._update_weights(input_vec, output, label, rate)
def _update_weights(self,input_vecs,output,labels,rate):
'''
Desc:
按照感知器规则更新权重
Args:
input_vec —— 输入向量
output —— 经过感知器规则计算得到的输出
label —— 输入向量对应的标签
rate —— 学习率
Returns:
None
'''
# 利用感知器规则更新权重
delta = labels -output
# map() 接收一个函数 f 和一个 list ,并通过把函数 f 依次作用在 list 的每个元素上,得到一个新的 list 返回。
# 比如我们的 f 函数是计算平方, map(f, [1,2,3,4,5]) ===> 返回 [1,4,9,16,25]
# zip() 接收任意多个(包括 0 个和 1个)序列作为参数,返回一个 tuple 列表。
# 例:x = [1,2,3] y = [4,5,6] z = [7,8,9] xyz = zip(x, y, z) ===> [(1,4,7), (2,5,8), (3,6,9)]
# 此处python3必须对map函数进行list操作,不然 self.weights为map类型,最后无法打印出具体数值
pack = zip(input_vecs,self.weights)
tmp = []
for (x,w) in pack:
tmp.append(w+x*delta*rate)
self.weights = tmp
# 更新 bias
self.bias = self.bias + delta*rate
#print("_update_weights() -------------")
#print("label - output = delta:" ,labels, output, delta)
#应该是labels
#print("weights ", self.weights)
#print("bias", self.bias)
def f(x):
'''
Desc:
定义激活函数 f
Args:
x —— 输入向量
Returns:
(实现阶跃函数)大于 0 返回 1,否则返回 0
'''
if x>=0:
return 1
else:
return 0
def get_training_dataset():
'''
Desc:
基于 and 真值表来构建/获取训练数据集
Args:
None
Returns:
input_vecs —— 输入向量
labels —— 输入向量对应的标签
'''
# 构建训练数据,输入向量的列表
input_vecs = [[1,1],[0,0],[1,0],[0,1]]
# 期望的输出列表,也就是上面的输入向量的列表中数据对应的标签,是一一对应的
input_vecs = [[0,0],[0,1],[0,2],[1,1],[1,0],[2,2],[2,4],[4,0],[3,3],[0,4]]
#labels = [1,0,0,0]
labels = [1,1,1,1,1,0,0,0,0,0]
return input_vecs,labels
def train_and_perceptron():
'''
Desc:
使用 and 真值表来训练我们的感知器
Args:
None
Returns:
p —— 返回训练好的感知器
'''
# 创建感知器,输入参数的个数是 2 个(因为 and 是个二元函数),激活函数为 f
p = Perceptron(2, f) #函数f作为参数,从而定义了激活函数
# 进行训练,迭代 10 轮,学习速率是我们设定的 rate ,为 0.1
input_vecs, labels = get_training_dataset()
p.train(input_vecs, labels, 10, 0.1)
# 返回训练好的感知器
return p
if __name__ == '__main__':
'''
Desc:
主函数,调用上面返回的训练好的感知器进行预测
Args:
None
Returns:
None
'''
# 训练 and 感知器
and_perceptron = train_and_perceptron()
#and_perceptron.weights = [1,1]
#and_perceptron.bias = -0.5
# 打印训练获得的权重
print(and_perceptron)
# 测试
# print('1 and 1 = %d' % and_perceptron.predict([1, 1]))
# print('0 and 0 = %d' % and_perceptron.predict([0, 0]))
# print('1 and 0 = %d' % and_perceptron.predict([1, 0]))
# print('0 and 1 = %d' % and_perceptron.predict([0, 1]))
k=-1
d=2.333
print('k=',k)
print('d=',d)
xdata=np.linspace(0,5)
plt.figure()
plt.plot(xdata,xdata*k+d,'r')
#input_vecs = [[0,0],[0,1],[0,2],[1,1],[1,0],[2,2],[2,4],[4,0],[3,3],[0,4]]
x1=[0,0,0,1,1]
y1=[0,1,2,1,0]
x2=[2,2,4,3,0]
y2=[2,4,0,3,4]
plt.plot(x1,y1,'bo')
plt.plot(x2,y2,'yo')
plt.show()
4. k近邻算法
一个样本在特征空间内的k个最近邻样本的大多数都属于某一类别,则这个样本就属于这一个类别。
k-近邻(kNN, k-NearestNeighbor)算法是一种基本分类与回归方法,我们这里只讨论分类问题中的 k-近邻算法。
一句话总结:近朱者赤近墨者黑!
k 近邻算法的输入为实例的特征向量,对应于特征空间的点;输出为实例的类别,可以取多类。k 近邻算法假设给定一个训练数据集,其中的实例类别已定。分类时,对新的实例,根据其 k 个最近邻的训练实例的类别,通过多数表决等方式进行预测。因此,k近邻算法不具有显式的学习过程。
k 近邻算法实际上利用训练数据集对特征向量空间进行划分,并作为其分类的“模型”。 k值的选择、距离度量以及分类决策规则是k近邻算法的三个基本要素。
4.1 KNN 场景
电影可以按照题材分类,那么如何区分 动作片 和 爱情片 呢?
- 动作片:打斗次数更多
- 爱情片:亲吻次数更多
基于电影中的亲吻、打斗出现的次数,使用 k-近邻算法构造程序,就可以自动划分电影的题材类型。
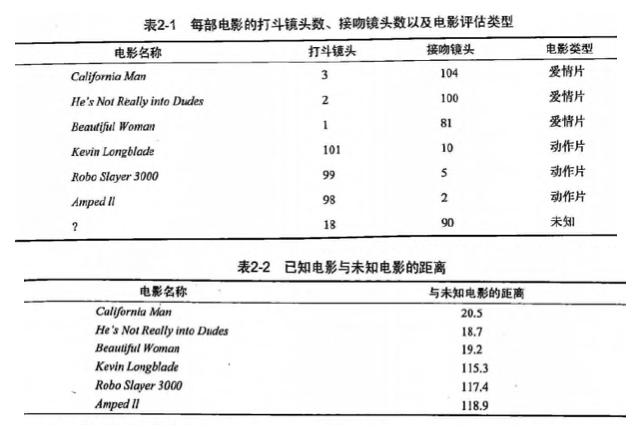
现在根据上面我们得到的样本集中所有电影与未知电影的距离,按照距离递增排序,可以找到 k 个距离最近的电影。
假定 k=3,则三个最靠近的电影依次是, He's Not Really into Dudes 、 Beautiful Woman 和 California Man。
knn 算法按照距离最近的三部电影的类型,决定未知电影的类型,而这三部电影全是爱情片,因此我们判定未知电影是爱情片。
4.2KNN 原理
KNN 工作原理
- 假设有一个带有标签的样本数据集(训练样本集),其中包含每条数据与所属分类的对应关系。
- 输入没有标签的新数据后,将新数据的每个特征与样本集中数据对应的特征进行比较。
- 计算新数据与样本数据集中每条数据的距离。
- 对求得的所有距离进行排序(从小到大,越小表示越相似)。
- 取前 k (k 一般小于等于 20 )个样本数据对应的分类标签。
- 求 k 个数据中出现次数最多的分类标签作为新数据的分类。
KNN 通俗理解
给定一个训练数据集,对新的输入实例,在训练数据集中找到与该实例最邻近的 k 个实例,这 k 个实例的多数属于某个类,就把该输入实例分为这个类。
KNN 开发流程
收集数据:任何方法
准备数据:距离计算所需要的数值,最好是结构化的数据格式
分析数据:任何方法
训练算法:此步骤不适用于 k-近邻算法
测试算法:计算错误率
使用算法:输入样本数据和结构化的输出结果,然后运行 k-近邻算法判断输入数据分类属于哪个分类,最后对计算出的分类执行后续处理
KNN 算法特点
优点:精度高、对异常值不敏感、无数据输入假定
缺点:计算复杂度高、空间复杂度高
适用数据范围:数值型和标称型
4.3项目案例1: 优化约会网站的配对效果
4.3.1项目概述
海伦使用约会网站寻找约会对象。经过一段时间之后,她发现曾交往过三种类型的人:
- 不喜欢的人
- 魅力一般的人
- 极具魅力的人
她希望:
- 工作日与魅力一般的人约会
- 周末与极具魅力的人约会
- 不喜欢的人则直接排除掉
现在她收集到了一些约会网站未曾记录的数据信息,这更有助于匹配对象的归类。
4.3.2开发流程
收集数据:提供文本文件
准备数据:使用 Python 解析文本文件
分析数据:使用 Matplotlib 画二维散点图
训练算法:此步骤不适用于 k-近邻算法
测试算法:使用海伦提供的部分数据作为测试样本。
测试样本和非测试样本的区别在于:
测试样本是已经完成分类的数据,如果预测分类与实际类别不同,则标记为一个错误。
使用算法:产生简单的命令行程序,然后海伦可以输入一些特征数据以判断对方是否为自己喜欢的类型。
收集数据:提供文本文件
海伦把这些约会对象的数据存放在文本文件 datingTestSet2.txt 中,总共有 1000 行。海伦约会的对象主要包含以下 3 种特征:
- 每年获得的飞行常客里程数
- 玩视频游戏所耗时间百分比
- 每周消费的冰淇淋公升数
文本文件数据格式如下:
40920 8.326976 0.953952 3
14488 7.153469 1.673904 2
26052 1.441871 0.805124 1
75136 13.147394 0.428964 1
38344 1.669788 0.134296 1
准备数据:使用 Python 解析文本文件
将文本记录转换为 NumPy 的解析程序
def file2matrix(filename):
"""
Desc:
导入训练数据
parameters:
filename: 数据文件路径
return:
数据矩阵 returnMat 和对应的类别 classLabelVector
"""
fr = open(filename)
# 获得文件中的数据行的行数
numberOfLines = len(fr.readlines())
# 生成对应的空矩阵
# 例如:zeros(2,3)就是生成一个 2*3的矩阵,各个位置上全是 0
returnMat = zeros((numberOfLines, 3)) # prepare matrix to return
classLabelVector = [] # prepare labels return
fr = open(filename)
index = 0
for line in fr.readlines():
# str.strip([chars]) --返回移除字符串头尾指定的字符生成的新字符串
line = line.strip()
# 以 '\t' 切割字符串
listFromLine = line.split('\t')
# 每列的属性数据
returnMat[index, :] = listFromLine[0:3]
# 每列的类别数据,就是 label 标签数据
classLabelVector.append(int(listFromLine[-1]))
index += 1
# 返回数据矩阵returnMat和对应的类别classLabelVector
return returnMat, classLabelVector
分析数据:使用 Matplotlib 画二维散点图
import matplotlib
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(datingDataMat[:, 1], datingDataMat[:, 2], 15.0*array(datingLabels), 15.0*array(datingLabels))
plt.show()
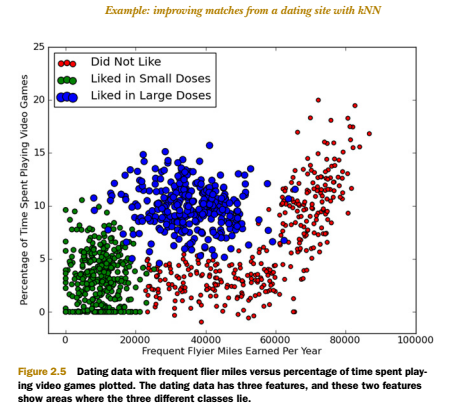
下图中采用矩阵的第一和第三列属性得到很好的展示效果,清晰地标识了三个不同的样本分类区域,具有不同爱好的人其类别区域也不同。
- 归一化数据 (归一化是一个让权重变为统一的过程,更多细节请参考: https://www.zhihu.com/question/19951858 )
| 序号 | 玩视频游戏所耗时间百分比 | 每年获得的飞行常客里程数 | 每周消费的冰淇淋公升数 | 样本分类 |
|---|---|---|---|---|
| 1 | 0.8 | 400 | 0.5 | 1 |
| 2 | 12 | 134 000 | 0.9 | 3 |
| 3 | 0 | 20 000 | 1.1 | 2 |
| 4 | 67 | 32 000 | 0.1 | 2 |
样本3和样本4的距离:
(0−67)2+(20000−32000)2+(1.1−0.1)2−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−√(0−67)2+(20000−32000)2+(1.1−0.1)2
归一化特征值,消除特征之间量级不同导致的影响
归一化定义: 我是这样认为的,归一化就是要把你需要处理的数据经过处理后(通过某种算法)限制在你需要的一定范围内。首先归一化是为了后面数据处理的方便,其次是保正程序运行时收敛加快。 方法有如下:
-
线性函数转换,表达式如下:
y=(x-MinValue)/(MaxValue-MinValue)
说明:x、y分别为转换前、后的值,MaxValue、MinValue分别为样本的最大值和最小值。
-
对数函数转换,表达式如下:
y=log10(x)
说明:以10为底的对数函数转换。
-
反余切函数转换,表达式如下:
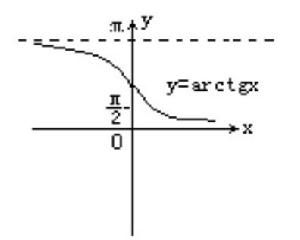
y=atan(x)*2/PI
-
式(1)将输入值换算为[-1,1]区间的值,在输出层用式(2)换算回初始值,其中和分别表示训练样本集中负荷的最大值和最小值。
在统计学中,归一化的具体作用是归纳统一样本的统计分布性。归一化在0-1之间是统计的概率分布,归一化在-1–+1之间是统计的坐标分布。
def autoNorm(dataSet):
"""
Desc:
归一化特征值,消除特征之间量级不同导致的影响
parameter:
dataSet: 数据集
return:
归一化后的数据集 normDataSet. ranges和minVals即最小值与范围,并没有用到
归一化公式:
Y = (X-Xmin)/(Xmax-Xmin)
其中的 min 和 max 分别是数据集中的最小特征值和最大特征值。该函数可以自动将数字特征值转化为0到1的区间。
"""
# 计算每种属性的最大值、最小值、范围
minVals = dataSet.min(0)
maxVals = dataSet.max(0)
# 极差
ranges = maxVals - minVals
normDataSet = zeros(shape(dataSet))
m = dataSet.shape[0]
# 生成与最小值之差组成的矩阵
normDataSet = dataSet - tile(minVals, (m, 1))
# 将最小值之差除以范围组成矩阵
normDataSet = normDataSet / tile(ranges, (m, 1)) # element wise divide
return normDataSet, ranges, minVals
训练算法:此步骤不适用于 k-近邻算法
因为测试数据每一次都要与全量的训练数据进行比较,所以这个过程是没有必要的。
测试算法:使用海伦提供的部分数据作为测试样本。如果预测分类与实际类别不同,则标记为一个错误。
kNN 分类器针对约会网站的测试代码
def datingClassTest():
"""
Desc:
对约会网站的测试方法
parameters:
none
return:
错误数
"""
# 设置测试数据的的一个比例(训练数据集比例=1-hoRatio)
hoRatio = 0.1 # 测试范围,一部分测试一部分作为样本
# 从文件中加载数据
datingDataMat, datingLabels = file2matrix('input/2.KNN/datingTestSet2.txt') # load data setfrom file
# 归一化数据
normMat, ranges, minVals = autoNorm(datingDataMat)
# m 表示数据的行数,即矩阵的第一维
m = normMat.shape[0]
# 设置测试的样本数量, numTestVecs:m表示训练样本的数量
numTestVecs = int(m * hoRatio)
print 'numTestVecs=', numTestVecs
errorCount = 0.0
for i in range(numTestVecs):
# 对数据测试
classifierResult = classify0(normMat[i, :], normMat[numTestVecs:m, :], datingLabels[numTestVecs:m], 3)
print "the classifier came back with: %d, the real answer is: %d" % (classifierResult, datingLabels[i])
if (classifierResult != datingLabels[i]): errorCount += 1.0
print "the total error rate is: %f" % (errorCount / float(numTestVecs))
print errorCount
使用算法:产生简单的命令行程序,然后海伦可以输入一些特征数据以判断对方是否为自己喜欢的类型。
约会网站预测函数
def clasdifyPerson():
resultList = ['not at all', 'in small doses', 'in large doses']
percentTats = float(raw_input("percentage of time spent playing video games ?"))
ffMiles = float(raw_input("frequent filer miles earned per year?"))
iceCream = float(raw_input("liters of ice cream consumed per year?"))
datingDataMat, datingLabels = file2matrix('datingTestSet2.txt')
normMat, ranges, minVals = autoNorm(datingDataMat)
inArr = array([ffMils, percentTats, iceCream])
classifierResult = classify0((inArr-minVals)/ranges,normMat,datingLabels, 3)
print "You will probably like this person: ", resultList[classifierResult - 1]
实际运行效果如下:
>>> kNN.classifyPerson()
percentage of time spent playing video games?10
frequent flier miles earned per year?10000
liters of ice cream consumed per year?0.5
You will probably like this person: in small doses
完整代码地址: https://github.com/apachecn/MachineLearning/blob/master/src/python/2.KNN/kNN.py
4.4项目案例2: 手写数字识别系统
4.4.1项目概述
构造一个能识别数字 0 到 9 的基于 KNN 分类器的手写数字识别系统。
需要识别的数字是存储在文本文件中的具有相同的色彩和大小:宽高是 32 像素 * 32 像素的黑白图像。
4.4.2开发流程
收集数据:提供文本文件。
准备数据:编写函数 img2vector(), 将图像格式转换为分类器使用的向量格式
分析数据:在 Python 命令提示符中检查数据,确保它符合要求
训练算法:此步骤不适用于 KNN
测试算法:编写函数使用提供的部分数据集作为测试样本,测试样本与非测试样本的
区别在于测试样本是已经完成分类的数据,如果预测分类与实际类别不同,
则标记为一个错误
使用算法:本例没有完成此步骤,若你感兴趣可以构建完整的应用程序,从图像中提取
数字,并完成数字识别,美国的邮件分拣系统就是一个实际运行的类似系统
收集数据: 提供文本文件
目录 trainingDigits 中包含了大约 2000 个例子,每个例子内容如下图所示,每个数字大约有 200 个样本;目录 testDigits 中包含了大约 900 个测试数据。
准备数据: 编写函数 img2vector(), 将图像文本数据转换为分类器使用的向量
将图像文本数据转换为向量
def img2vector(filename):
returnVect = zeros((1,1024))
fr = open(filename)
for i in range(32):
lineStr = fr.readLine()
for j in range(32):
returnVect[0,32*i+j] = int(lineStr[j])
return returnVect
分析数据:在 Python 命令提示符中检查数据,确保它符合要求
在 Python 命令行中输入下列命令测试 img2vector 函数,然后与文本编辑器打开的文件进行比较:
>>> testVector = kNN.img2vector('testDigits/0_13.txt')
>>> testVector[0,0:31]
array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 1., 1., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])
>>> testVector[0,31:63]
array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 1., 1., 1., 1., 1., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])
训练算法:此步骤不适用于 KNN
因为测试数据每一次都要与全量的训练数据进行比较,所以这个过程是没有必要的。
测试算法:编写函数使用提供的部分数据集作为测试样本,如果预测分类与实际类别不同,则标记为一个错误
def handwritingClassTest():
# 1. 导入训练数据
hwLabels = []
trainingFileList = listdir('input/2.KNN/trainingDigits') # load the training set
m = len(trainingFileList)
trainingMat = zeros((m, 1024))
# hwLabels存储0~9对应的index位置, trainingMat存放的每个位置对应的图片向量
for i in range(m):
fileNameStr = trainingFileList[i]
fileStr = fileNameStr.split('.')[0] # take off .txt
classNumStr = int(fileStr.split('_')[0])
hwLabels.append(classNumStr)
# 将 32*32的矩阵->1*1024的矩阵
trainingMat[i, :] = img2vector('input/2.KNN/trainingDigits/%s' % fileNameStr)
# 2. 导入测试数据
testFileList = listdir('input/2.KNN/testDigits') # iterate through the test set
errorCount = 0.0
mTest = len(testFileList)
for i in range(mTest):
fileNameStr = testFileList[i]
fileStr = fileNameStr.split('.')[0] # take off .txt
classNumStr = int(fileStr.split('_')[0])
vectorUnderTest = img2vector('input/2.KNN/testDigits/%s' % fileNameStr)
classifierResult = classify0(vectorUnderTest, trainingMat, hwLabels, 3)
print "the classifier came back with: %d, the real answer is: %d" % (classifierResult, classNumStr)
if (classifierResult != classNumStr): errorCount += 1.0
print "\nthe total number of errors is: %d" % errorCount
print "\nthe total error rate is: %f" % (errorCount / float(mTest))
使用算法:本例没有完成此步骤,若你感兴趣可以构建完整的应用程序,从图像中提取数字,并完成数字识别,美国的邮件分拣系统就是一个实际运行的类似系统
完整代码地址: https://github.com/apachecn/MachineLearning/blob/master/src/python/2.KNN/kNN.py
4.5KNN 小结
经过上面的介绍我们可以知道, k 近邻算法有 三个基本的要素:
- k 值的选择
- k 值的选择会对 k 近邻算法的结果产生重大的影响。
- 如果选择较小的 k 值,就相当于用较小的邻域中的训练实例进行预测,“学习”的近似误差(approximation error)会减小,只有与输入实例较近的(相似的)训练实例才会对预测结果起作用。但缺点是“学习”的估计误差(estimation error)会增大,预测结果会对近邻的实例点非常敏感。如果邻近的实例点恰巧是噪声,预测就会出错。换句话说,k 值的减小就意味着整体模型变得复杂,容易发生过拟合。
- 如果选择较大的 k 值,就相当于用较大的邻域中的训练实例进行预测。其优点是可以减少学习的估计误差。但缺点是学习的近似误差会增大。这时与输入实例较远的(不相似的)训练实例也会对预测起作用,使预测发生错误。 k 值的增大就意味着整体的模型变得简单。
- 近似误差和估计误差,请看这里:https://www.zhihu.com/question/60793482
- 距离度量
- 分类决策规则
- k 近邻算法中的分类决策规则往往是多数表决,即由输入实例的 k 个邻近的训练实例中的多数类决定输入实例的类。
- 作者:羊三 小瑶
- GitHub地址: https://github.com/apachecn/MachineLearning
- 版权声明:欢迎转载学习 => 请标注信息来源于 ApacheCN
5.决策树
决策树(Decision Tree)算法是一种基本的分类与回归方法,是最经常使用的数据挖掘算法之一。我们这章节只讨论用于分类的决策树。
决策树模型呈树形结构,在分类问题中,表示基于特征对实例进行分类的过程。它可以认为是 if-then 规则的集合,也可以认为是定义在特征空间与类空间上的条件概率分布。
决策树学习通常包括 3 个步骤:特征选择、决策树的生成和决策树的修剪。
决策树 场景
一个叫做 “二十个问题” 的游戏,游戏的规则很简单:参与游戏的一方在脑海中想某个事物,其他参与者向他提问,只允许提 20 个问题,问题的答案也只能用对或错回答。问问题的人通过推断分解,逐步缩小待猜测事物的范围,最后得到游戏的答案。
一个邮件分类系统,大致工作流程如下:
首先检测发送邮件域名地址。如果地址为 myEmployer.com, 则将其放在分类 "无聊时需要阅读的邮件"中。
如果邮件不是来自这个域名,则检测邮件内容里是否包含单词 "曲棍球" , 如果包含则将邮件归类到 "需要及时处理的朋友邮件",
如果不包含则将邮件归类到 "无需阅读的垃圾邮件" 。
决策树的定义:
分类决策树模型是一种描述对实例进行分类的树形结构。决策树由结点(node)和有向边(directed edge)组成。结点有两种类型:内部结点(internal node)和叶结点(leaf node)。内部结点表示一个特征或属性,叶结点表示一个类。
用决策树分类,从根节点开始,对实例的某一特征进行测试,根据测试结果,将实例分配到其子结点;这时,每一个子结点对应着该特征的一个取值。如此递归地对实例进行测试并分配,直至达到叶结点。最后将实例分配到叶结点的类中。
决策树 原理
决策树 须知概念
信息熵 & 信息增益
熵: 熵(entropy)指的是体系的混乱的程度,在不同的学科中也有引申出的更为具体的定义,是各领域十分重要的参量。
信息熵(香农熵): 是一种信息的度量方式,表示信息的混乱程度,也就是说:信息越有序,信息熵越低。例如:火柴有序放在火柴盒里,熵值很低,相反,熵值很高。
信息增益: 在划分数据集前后信息发生的变化称为信息增益。
决策树 工作原理
如何构造一个决策树? 我们使用 createBranch() 方法,如下所示:
检测数据集中的所有数据的分类标签是否相同:
If so return 类标签
Else:
寻找划分数据集的最好特征(划分之后信息熵最小,也就是信息增益最大的特征)
划分数据集
创建分支节点
for 每个划分的子集
调用函数 createBranch (创建分支的函数)并增加返回结果到分支节点中
return 分支节点
决策树 开发流程
收集数据:可以使用任何方法。
准备数据:树构造算法只适用于标称型数据,因此数值型数据必须离散化。
分析数据:可以使用任何方法,构造树完成之后,我们应该检查图形是否符合预期。
训练算法:构造树的数据结构。
测试算法:使用经验树计算错误率。(经验树没有搜索到较好的资料,有兴趣的同学可以来补充)
使用算法:此步骤可以适用于任何监督学习算法,而使用决策树可以更好地理解数据的内在含义。
决策树 算法特点
优点:计算复杂度不高,输出结果易于理解,对中间值的缺失不敏感,可以处理不相关特征数据。
缺点:可能会产生过度匹配问题。
适用数据类型:数值型和标称型。
决策树 项目案例
项目案例1: 判定鱼类和非鱼类
项目概述
根据以下 2 个特征,将动物分成两类:鱼类和非鱼类。
特征:
- 不浮出水面是否可以生存
- 是否有脚蹼
开发流程
收集数据:可以使用任何方法
准备数据:树构造算法只适用于标称型数据,因此数值型数据必须离散化
分析数据:可以使用任何方法,构造树完成之后,我们应该检查图形是否符合预期
训练算法:构造树的数据结构
测试算法:使用决策树执行分类
使用算法:此步骤可以适用于任何监督学习算法,而使用决策树可以更好地理解数据的内在含义
收集数据:可以使用任何方法
我们利用 createDataSet() 函数输入数据
def createDataSet():
dataSet = [[1, 1, 'yes'],
[1, 1, 'yes'],
[1, 0, 'no'],
[0, 1, 'no'],
[0, 1, 'no']]
labels = ['no surfacing', 'flippers']
return dataSet, labels
准备数据:树构造算法只适用于标称型数据,因此数值型数据必须离散化
此处,由于我们输入的数据本身就是离散化数据,所以这一步就省略了。
分析数据:可以使用任何方法,构造树完成之后,我们应该检查图形是否符合预期
计算给定数据集的香农熵的函数
def calcShannonEnt(dataSet):
# 求list的长度,表示计算参与训练的数据量
numEntries = len(dataSet)
# 计算分类标签label出现的次数
labelCounts = {}
# the the number of unique elements and their occurance
for featVec in dataSet:
# 将当前实例的标签存储,即每一行数据的最后一个数据代表的是标签
currentLabel = featVec[-1]
# 为所有可能的分类创建字典,如果当前的键值不存在,则扩展字典并将当前键值加入字典。每个键值都记录了当前类别出现的次数。
if currentLabel not in labelCounts.keys():
labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
# 对于 label 标签的占比,求出 label 标签的香农熵
shannonEnt = 0.0
for key in labelCounts:
# 使用所有类标签的发生频率计算类别出现的概率。
prob = float(labelCounts[key])/numEntries
# 计算香农熵,以 2 为底求对数
shannonEnt -= prob * log(prob, 2)
return shannonEnt
按照给定特征划分数据集
将指定特征的特征值等于 value 的行剩下列作为子数据集。
def splitDataSet(dataSet, index, value):
"""splitDataSet(通过遍历dataSet数据集,求出index对应的colnum列的值为value的行)
就是依据index列进行分类,如果index列的数据等于 value的时候,就要将 index 划分到我们创建的新的数据集中
Args:
dataSet 数据集 待划分的数据集
index 表示每一行的index列 划分数据集的特征
value 表示index列对应的value值 需要返回的特征的值。
Returns:
index列为value的数据集【该数据集需要排除index列】
"""
retDataSet = []
for featVec in dataSet:
# index列为value的数据集【该数据集需要排除index列】
# 判断index列的值是否为value
if featVec[index] == value:
# chop out index used for splitting
# [:index]表示前index行,即若 index 为2,就是取 featVec 的前 index 行
reducedFeatVec = featVec[:index]
'''
请百度查询一下: extend和append的区别
list.append(object) 向列表中添加一个对象object
list.extend(sequence) 把一个序列seq的内容添加到列表中
1、使用append的时候,是将new_media看作一个对象,整体打包添加到music_media对象中。
2、使用extend的时候,是将new_media看作一个序列,将这个序列和music_media序列合并,并放在其后面。
result = []
result.extend([1,2,3])
print result
result.append([4,5,6])
print result
result.extend([7,8,9])
print result
结果:
[1, 2, 3]
[1, 2, 3, [4, 5, 6]]
[1, 2, 3, [4, 5, 6], 7, 8, 9]
'''
reducedFeatVec.extend(featVec[index+1:])
# [index+1:]表示从跳过 index 的 index+1行,取接下来的数据
# 收集结果值 index列为value的行【该行需要排除index列】
retDataSet.append(reducedFeatVec)
return retDataSet
选择最好的数据集划分方式
def chooseBestFeatureToSplit(dataSet):
"""chooseBestFeatureToSplit(选择最好的特征)
Args:
dataSet 数据集
Returns:
bestFeature 最优的特征列
"""
# 求第一行有多少列的 Feature, 最后一列是label列嘛
numFeatures = len(dataSet[0]) - 1
# 数据集的原始信息熵
baseEntropy = calcShannonEnt(dataSet)
# 最优的信息增益值, 和最优的Featurn编号
bestInfoGain, bestFeature = 0.0, -1
# iterate over all the features
for i in range(numFeatures):
# create a list of all the examples of this feature
# 获取对应的feature下的所有数据
featList = [example[i] for example in dataSet]
# get a set of unique values
# 获取剔重后的集合,使用set对list数据进行去重
uniqueVals = set(featList)
# 创建一个临时的信息熵
newEntropy = 0.0
# 遍历某一列的value集合,计算该列的信息熵
# 遍历当前特征中的所有唯一属性值,对每个唯一属性值划分一次数据集,计算数据集的新熵值,并对所有唯一特征值得到的熵求和。
for value in uniqueVals:
subDataSet = splitDataSet(dataSet, i, value)
# 计算概率
prob = len(subDataSet)/float(len(dataSet))
# 计算信息熵
newEntropy += prob * calcShannonEnt(subDataSet)
# gain[信息增益]: 划分数据集前后的信息变化, 获取信息熵最大的值
# 信息增益是熵的减少或者是数据无序度的减少。最后,比较所有特征中的信息增益,返回最好特征划分的索引值。
infoGain = baseEntropy - newEntropy
print 'infoGain=', infoGain, 'bestFeature=', i, baseEntropy, newEntropy
if (infoGain > bestInfoGain):
bestInfoGain = infoGain
bestFeature = i
return bestFeature
问:上面的 newEntropy 为什么是根据子集计算的呢?
答:因为我们在根据一个特征计算香农熵的时候,该特征的分类值是相同,这个特征这个分类的香农熵为 0;
这就是为什么计算新的香农熵的时候使用的是子集。
训练算法:构造树的数据结构
创建树的函数代码如下:
def createTree(dataSet, labels):
classList = [example[-1] for example in dataSet]
# 如果数据集的最后一列的第一个值出现的次数=整个集合的数量,也就说只有一个类别,就只直接返回结果就行
# 第一个停止条件:所有的类标签完全相同,则直接返回该类标签。
# count() 函数是统计括号中的值在list中出现的次数
if classList.count(classList[0]) == len(classList):
return classList[0]
# 如果数据集只有1列,那么最初出现label次数最多的一类,作为结果
# 第二个停止条件:使用完了所有特征,仍然不能将数据集划分成仅包含唯一类别的分组。
if len(dataSet[0]) == 1:
return majorityCnt(classList)
# 选择最优的列,得到最优列对应的label含义
bestFeat = chooseBestFeatureToSplit(dataSet)
# 获取label的名称
bestFeatLabel = labels[bestFeat]
# 初始化myTree
myTree = {bestFeatLabel: {}}
# 注:labels列表是可变对象,在PYTHON函数中作为参数时传址引用,能够被全局修改
# 所以这行代码导致函数外的同名变量被删除了元素,造成例句无法执行,提示'no surfacing' is not in list
del(labels[bestFeat])
# 取出最优列,然后它的branch做分类
featValues = [example[bestFeat] for example in dataSet]
uniqueVals = set(featValues)
for value in uniqueVals:
# 求出剩余的标签label
subLabels = labels[:]
# 遍历当前选择特征包含的所有属性值,在每个数据集划分上递归调用函数createTree()
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels)
# print 'myTree', value, myTree
return myTree
测试算法:使用决策树执行分类
def classify(inputTree, featLabels, testVec):
"""classify(给输入的节点,进行分类)
Args:
inputTree 决策树模型
featLabels Feature标签对应的名称
testVec 测试输入的数据
Returns:
classLabel 分类的结果值,需要映射label才能知道名称
"""
# 获取tree的根节点对于的key值
firstStr = inputTree.keys()[0]
# 通过key得到根节点对应的value
secondDict = inputTree[firstStr]
# 判断根节点名称获取根节点在label中的先后顺序,这样就知道输入的testVec怎么开始对照树来做分类
featIndex = featLabels.index(firstStr)
# 测试数据,找到根节点对应的label位置,也就知道从输入的数据的第几位来开始分类
key = testVec[featIndex]
valueOfFeat = secondDict[key]
print '+++', firstStr, 'xxx', secondDict, '---', key, '>>>', valueOfFeat
# 判断分枝是否结束: 判断valueOfFeat是否是dict类型
if isinstance(valueOfFeat, dict):
classLabel = classify(valueOfFeat, featLabels, testVec)
else:
classLabel = valueOfFeat
return classLabel
使用算法:此步骤可以适用于任何监督学习算法,而使用决策树可以更好地理解数据的内在含义。
完整代码地址: https://github.com/apachecn/MachineLearning/blob/master/src/python/3.DecisionTree/DecisionTree.py
项目案例2: 使用决策树预测隐形眼镜类型
项目概述
隐形眼镜类型包括硬材质、软材质以及不适合佩戴隐形眼镜。我们需要使用决策树预测患者需要佩戴的隐形眼镜类型。
开发流程
- 收集数据: 提供的文本文件。
- 解析数据: 解析 tab 键分隔的数据行
- 分析数据: 快速检查数据,确保正确地解析数据内容,使用 createPlot() 函数绘制最终的树形图。
- 训练算法: 使用 createTree() 函数。
- 测试算法: 编写测试函数验证决策树可以正确分类给定的数据实例。
- 使用算法: 存储树的数据结构,以便下次使用时无需重新构造树。
收集数据:提供的文本文件
文本文件数据格式如下:
young myope no reduced no lenses
pre myope no reduced no lenses
presbyopic myope no reduced no lenses
解析数据:解析 tab 键分隔的数据行
lecses = [inst.strip().split('\t') for inst in fr.readlines()]
lensesLabels = ['age', 'prescript', 'astigmatic', 'tearRate']
分析数据:快速检查数据,确保正确地解析数据内容,使用 createPlot() 函数绘制最终的树形图。
>>> treePlotter.createPlot(lensesTree)
训练算法:使用 createTree() 函数
>>> lensesTree = trees.createTree(lenses, lensesLabels)
>>> lensesTree
{'tearRate': {'reduced': 'no lenses', 'normal': {'astigmatic':{'yes':
{'prescript':{'hyper':{'age':{'pre':'no lenses', 'presbyopic':
'no lenses', 'young':'hard'}}, 'myope':'hard'}}, 'no':{'age':{'pre':
'soft', 'presbyopic':{'prescript': {'hyper':'soft', 'myope':
'no lenses'}}, 'young':'soft'}}}}}
测试算法: 编写测试函数验证决策树可以正确分类给定的数据实例。
使用算法: 存储树的数据结构,以便下次使用时无需重新构造树。
使用 pickle 模块存储决策树
def storeTree(inputTree, filename):
impory pickle
fw = open(filename, 'w')
pickle.dump(inputTree, fw)
fw.close()
def grabTree(filename):
import pickle
fr = open(filename)
return pickle.load(fr)
完整代码地址: https://github.com/apachecn/MachineLearning/blob/master/src/python/3.DecisionTree/DecisionTree.py
- 作者:片刻 小瑶
- GitHub地址: https://github.com/apachecn/MachineLearning
- 版权声明:欢迎转载学习 => 请标注信息来源于 ApacheCN
6.SVM
支持向量机 概述
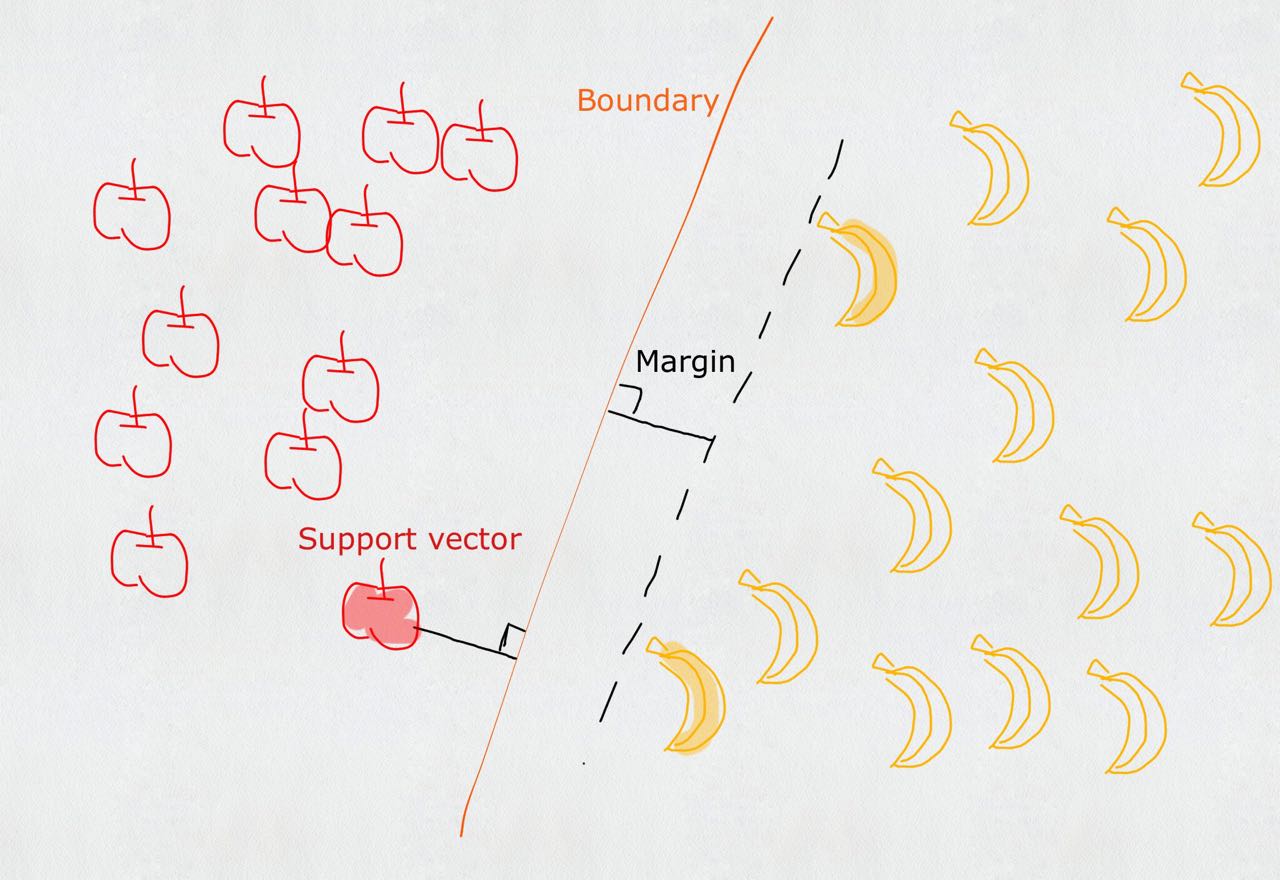
支持向量机(Support Vector Machines, SVM):是一种机器学习算法。
- 支持向量(Support Vector)就是离分隔超平面最近的那些点。
- 机(Machine)就是表示一种算法,而不是表示机器。
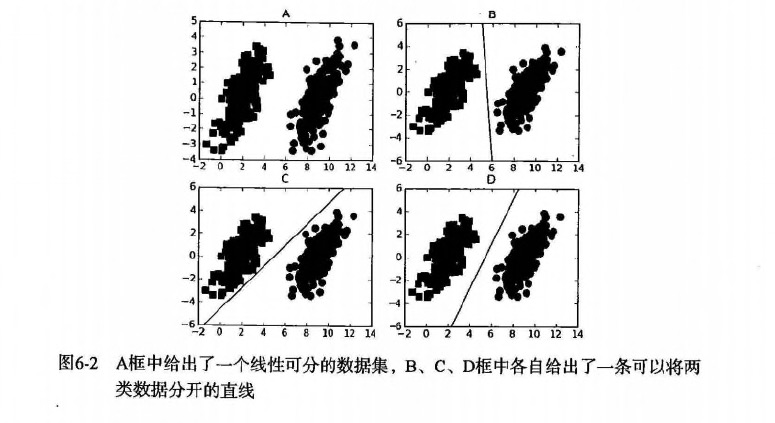
支持向量机 场景
- 要给左右两边的点进行分类
- 明显发现:选择D会比B、C分隔的效果要好很多。
支持向量机 原理
SVM 工作原理
对于上述的苹果和香蕉,我们想象为2种水果类型的炸弹。(保证距离最近的炸弹,距离它们最远)
- 寻找最大分类间距
- 转而通过拉格朗日函数求优化的问题
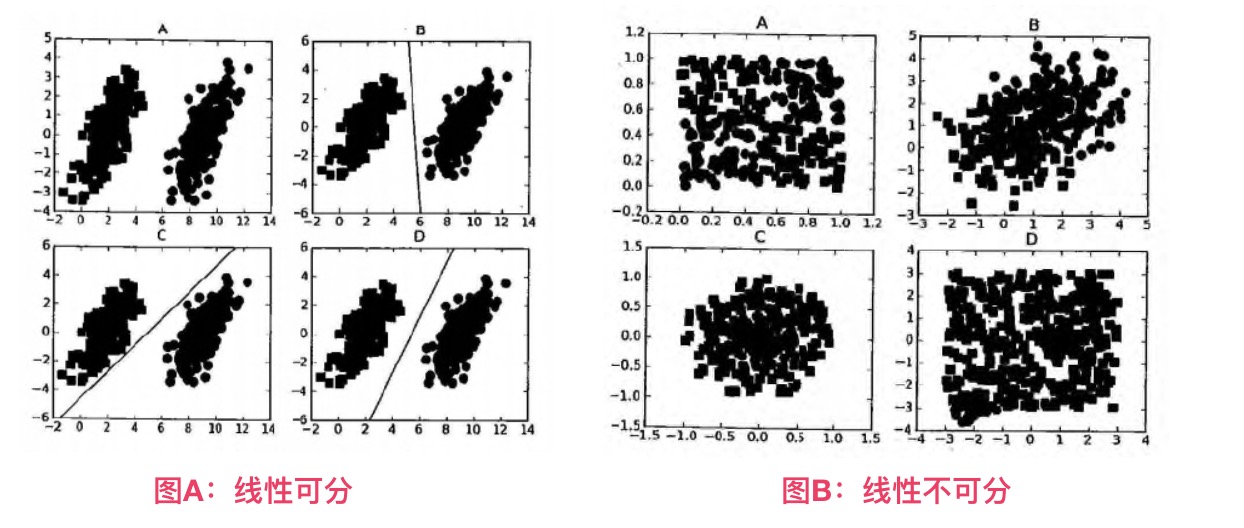
- 数据可以通过画一条直线就可以将它们完全分开,这组数据叫
线性可分(linearly separable)数据,而这条分隔直线称为分隔超平面(separating hyperplane)。 - 如果数据集上升到1024维呢?那么需要1023维来分隔数据集,也就说需要N-1维的对象来分隔,这个对象叫做
超平面(hyperlane),也就是分类的决策边界。
寻找最大间隔
为什么寻找最大间隔
摘录地址:http://slideplayer.com/slide/8610144 (第12条信息)
Support Vector Machines: Slide 12 Copyright © 2001, 2003, Andrew W. Moore Why Maximum Margin?
denotes +1 denotes -1 f(x,w,b) = sign(w. x - b) The maximum margin linear classifier is the linear classifier with the, um, maximum margin.
This is the simplest kind of SVM (Called an LSVM) Support Vectors are those datapoints that the margin pushes up against
1.Intuitively this feels safest.
2.If we’ve made a small error in the location of the boundary (it’s been jolted in its perpendicular direction) this gives us least chance of causing a misclassification.
3.CV is easy since the model is immune to removal of any non-support-vector datapoints.
4.There’s some theory that this is a good thing.
5.Empirically it works very very well.
* * *
1. 直觉上是安全的
2. 如果我们在边界的位置发生了一个小错误(它在垂直方向上被颠倒),这给我们最小的错误分类机会。
3. CV(Computer Vision 计算机视觉 - 这缩写看着可怕)很容易,因为该模型对任何非支持向量数据点的去除是免疫的。
4. 有一些理论,这是一件好事。
5. 通常它的工作非常好。
怎么寻找最大间隔
点到超平面的距离
- 分隔超平面
函数间距: y(x)=wTx+by(x)=wTx+b - 分类的结果: f(x)=sign(wTx+b)f(x)=sign(wTx+b) (sign表示>0为1,<0为-1,=0为0)
-
点到超平面的 几何间距: d(x)=(wTx+b)/w d(x)=(wTx+b)/ w ( w 表示w矩阵的二范式=> w∗wT−−−−−−√w∗wT, 点到超平面的距离也是类似的)
拉格朗日乘子法
-
类别标签用-1、1,是为了后期方便 lable∗(wTx+b)lable∗(wTx+b) 的标识和距离计算;如果 lable∗(wTx+b)>0lable∗(wTx+b)>0 表示预测正确,否则预测错误。
-
现在目标很明确,就是要找到
w和
b,因此我们必须要找到最小间隔的数据点,也就是前面所说的
支持向量。
-
也就说,让最小的距离取最大.(最小的距离:就是最小间隔的数据点;最大:就是最大间距,为了找出最优超平面–最终就是支持向量)
-
目标函数:
arg:max关于w,b(min[lable∗(wTx+b)]∗1 w )arg:max关于w,b(min[lable∗(wTx+b)]∗1 w ) -
如果 lable∗(wTx+b)>0lable∗(wTx+b)>0 表示预测正确,也称 函数间隔,w w 可以理解为归一化,也称 几何间隔。 - 令 lable∗(wTx+b)>=1lable∗(wTx+b)>=1, 因为0~1之间,得到的点是存在误判的可能性,所以要保障 min[lable∗(wTx+b)]=1min[lable∗(wTx+b)]=1,才能更好降低噪音数据影响。
-
所以本质上是求 arg:max关于w,b1 w arg:max关于w,b1 w ;也就说,我们约束(前提)条件是: lable∗(wTx+b)=1lable∗(wTx+b)=1
-
-
-
新的目标函数求解:
arg:max关于w,b1 w arg:max关于w,b1 w -
=> 就是求: arg:min关于w,b w arg:min关于w,b w (求矩阵会比较麻烦,如果x只是 12∗x212∗x2 的偏导数,那么。。同样是求最小值) -
=> 就是求: arg:min关于w,b(12∗ w 2)arg:min关于w,b(12∗ w 2) (二次函数求导,求极值,平方也方便计算) - 本质上就是求线性不等式的二次优化问题(求分隔超平面,等价于求解相应的凸二次规划问题)
-
-
通过拉格朗日乘子法,求二次优化问题
- 假设需要求极值的目标函数 (objective function) 为 f(x,y),限制条件为 φ(x,y)=M # M=1
- 设g(x,y)=M-φ(x,y) # 临时φ(x,y)表示下文中 label∗(wTx+b)label∗(wTx+b)
- 定义一个新函数: F(x,y,λ)=f(x,y)+λg(x,y)
- a为λ(a>=0),代表要引入的拉格朗日乘子(Lagrange multiplier)
-
那么: L(w,b,α)=12∗ w 2+∑i=1nαi∗[1−label∗(wTx+b)]L(w,b,α)=12∗ w 2+∑i=1nαi∗[1−label∗(wTx+b)] - 因为:label∗(wTx+b)>=1,α>=0label∗(wTx+b)>=1,α>=0 , 所以 α∗[1−label∗(wTx+b)]<=0α∗[1−label∗(wTx+b)]<=0 , ∑i=1nαi∗[1−label∗(wTx+b)]<=0∑i=1nαi∗[1−label∗(wTx+b)]<=0
- 当 label∗(wTx+b)>1label∗(wTx+b)>1 则 α=0α=0 ,表示该点为非支持向量
-
相当于求解: max关于αL(w,b,α)=12∗ w 2max关于αL(w,b,α)=12∗ w 2 -
如果求: min关于w,b12∗ w 2min关于w,b12∗ w 2 , 也就是要求: min关于w,b(max关于αL(w,b,α))min关于w,b(max关于αL(w,b,α))
-
现在转化到对偶问题的求解
- min关于w,b(max关于αL(w,b,α))min关于w,b(max关于αL(w,b,α)) >= max关于α(min关于w,b L(w,b,α))max关于α(min关于w,b L(w,b,α))
- 现在分2步
-
先求: min关于w,bL(w,b,α)=12∗ w 2+∑i=1nαi∗[1−label∗(wTx+b)]min关于w,bL(w,b,α)=12∗ w 2+∑i=1nαi∗[1−label∗(wTx+b)] - 就是求
L(w,b,a)关于[w, b]的偏导数, 得到w和b的值,并化简为:L和a的方程。 - 参考: 如果公式推导还是不懂,也可以参考《统计学习方法》李航-P103<学习的对偶算法> [](https://img.cntofu.com/book/MachineLearning/images/6.SVM/SVM_5_Lagrangemultiplier.png)
-
终于得到课本上的公式: max关于α(∑i=1mαi−12∑i,j=1mlabeli⋅labelj⋅αi⋅αj⋅<xi,xj>)max关于α(∑i=1mαi−12∑i,j=1mlabeli·labelj·αi·αj·<xi,xj>)
-
约束条件: a>=0a>=0 并且 ∑mi=1ai⋅labeli=0∑i=1mai·labeli=0
松弛变量(slack variable)
参考地址:http://blog.csdn.net/wusecaiyun/article/details/49659183
-
我们知道几乎所有的数据都不那么干净, 通过引入松弛变量来
允许数据点可以处于分隔面错误的一侧。 -
约束条件: C>=a>=0C>=a>=0 并且 ∑mi=1ai⋅labeli=0∑i=1mai·labeli=0
-
总的来说:
-
常量C是
惩罚因子, 表示离群点的权重(用于控制“最大化间隔”和“保证大部分点的函数间隔小于1.0” )
- label∗(wTx+b)>1label∗(wTx+b)>1 and alpha = 0 (在边界外,就是非支持向量)
- label∗(wTx+b)=1label∗(wTx+b)=1 and 0< alpha < C (在分割超平面上,就支持向量)
- label∗(wTx+b)<1label∗(wTx+b)<1 and alpha = C (在分割超平面内,是误差点 -> C表示它该受到的惩罚因子程度)
- 参考地址:https://www.zhihu.com/question/48351234/answer/110486455
-
C值越大,表示离群点影响越大,就越容易过度拟合;反之有可能欠拟合。
-
我们看到,目标函数控制了离群点的数目和程度,使大部分样本点仍然遵守限制条件。
-
例如:正类有10000个样本,而负类只给了100个(C越大表示100个负样本的影响越大,就会出现过度拟合,所以C决定了负样本对模型拟合程度的影响!,C就是一个非常关键的优化点!)
-
这一结论十分直接,SVM中的主要工作就是要求解 alpha.
SMO 高效优化算法
- SVM有很多种实现,最流行的一种实现是:
序列最小优化(Sequential Minimal Optimization, SMO)算法。 - 下面还会介绍一种称为
核函数(kernel)的方式将SVM扩展到更多数据集上。 - 注意:
SVM几何含义比较直观,但其算法实现较复杂,牵扯大量数学公式的推导。
序列最小优化(Sequential Minimal Optimization, SMO)
- 创建作者:John Platt
- 创建时间:1996年
- SMO用途:用于训练 SVM
- SMO目标:求出一系列 alpha 和 b,一旦求出 alpha,就很容易计算出权重向量 w 并得到分隔超平面。
- SMO思想:是将大优化问题分解为多个小优化问题来求解的。
- SMO原理:每次循环选择两个 alpha 进行优化处理,一旦找出一对合适的 alpha,那么就增大一个同时减少一个。
- 这里指的合适必须要符合一定的条件
- 这两个 alpha 必须要在间隔边界之外
- 这两个 alpha 还没有进行过区间化处理或者不在边界上。
- 之所以要同时改变2个 alpha;原因是我们有一个约束条件: ∑mi=1ai⋅labeli=0∑i=1mai·labeli=0;如果只是修改一个 alpha,很可能导致约束条件失效。
- 这里指的合适必须要符合一定的条件
SMO 伪代码大致如下:
创建一个 alpha 向量并将其初始化为0向量
当迭代次数小于最大迭代次数时(外循环)
对数据集中的每个数据向量(内循环):
如果该数据向量可以被优化
随机选择另外一个数据向量
同时优化这两个向量
如果两个向量都不能被优化,退出内循环
如果所有向量都没被优化,增加迭代数目,继续下一次循环
SVM 开发流程
收集数据:可以使用任意方法。
准备数据:需要数值型数据。
分析数据:有助于可视化分隔超平面。
训练算法:SVM的大部分时间都源自训练,该过程主要实现两个参数的调优。
测试算法:十分简单的计算过程就可以实现。
使用算法:几乎所有分类问题都可以使用SVM,值得一提的是,SVM本身是一个二类分类器,对多类问题应用SVM需要对代码做一些修改。
SVM 算法特点
优点:泛化(由具体的、个别的扩大为一般的,就是说:模型训练完后的新样本)错误率低,计算开销不大,结果易理解。
缺点:对参数调节和核函数的选择敏感,原始分类器不加修改仅适合于处理二分类问题。
使用数据类型:数值型和标称型数据。
课本案例(无核函数)
项目概述
对小规模数据点进行分类
开发流程
收集数据
文本文件格式:
3.542485 1.977398 -1
3.018896 2.556416 -1
7.551510 -1.580030 1
2.114999 -0.004466 -1
8.127113 1.274372 1
准备数据
def loadDataSet(fileName):
"""
对文件进行逐行解析,从而得到第行的类标签和整个特征矩阵
Args:
fileName 文件名
Returns:
dataMat 特征矩阵
labelMat 类标签
"""
dataMat = []
labelMat = []
fr = open(fileName)
for line in fr.readlines():
lineArr = line.strip().split('\t')
dataMat.append([float(lineArr[0]), float(lineArr[1])])
labelMat.append(float(lineArr[2]))
return dataMat, labelMat
分析数据: 无
训练算法
def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
"""smoSimple
Args:
dataMatIn 特征集合
classLabels 类别标签
C 松弛变量(常量值),允许有些数据点可以处于分隔面的错误一侧。
控制最大化间隔和保证大部分的函数间隔小于1.0这两个目标的权重。
可以通过调节该参数达到不同的结果。
toler 容错率(是指在某个体系中能减小一些因素或选择对某个系统产生不稳定的概率。)
maxIter 退出前最大的循环次数
Returns:
b 模型的常量值
alphas 拉格朗日乘子
"""
dataMatrix = mat(dataMatIn)
# 矩阵转置 和 .T 一样的功能
labelMat = mat(classLabels).transpose()
m, n = shape(dataMatrix)
# 初始化 b和alphas(alpha有点类似权重值。)
b = 0
alphas = mat(zeros((m, 1)))
# 没有任何alpha改变的情况下遍历数据的次数
iter = 0
while (iter < maxIter):
# w = calcWs(alphas, dataMatIn, classLabels)
# print("w:", w)
# 记录alpha是否已经进行优化,每次循环时设为0,然后再对整个集合顺序遍历
alphaPairsChanged = 0
for i in range(m):
# print 'alphas=', alphas
# print 'labelMat=', labelMat
# print 'multiply(alphas, labelMat)=', multiply(alphas, labelMat)
# 我们预测的类别 y[i] = w^Tx[i]+b; 其中因为 w = Σ(1~n) a[n]*lable[n]*x[n]
fXi = float(multiply(alphas, labelMat).T*(dataMatrix*dataMatrix[i, :].T)) + b
# 预测结果与真实结果比对,计算误差Ei
Ei = fXi - float(labelMat[i])
# 约束条件 (KKT条件是解决最优化问题的时用到的一种方法。我们这里提到的最优化问题通常是指对于给定的某一函数,求其在指定作用域上的全局最小值)
# 0<=alphas[i]<=C,但由于0和C是边界值,我们无法进行优化,因为需要增加一个alphas和降低一个alphas。
# 表示发生错误的概率:labelMat[i]*Ei 如果超出了 toler, 才需要优化。至于正负号,我们考虑绝对值就对了。
'''
# 检验训练样本(xi, yi)是否满足KKT条件
yi*f(i) >= 1 and alpha = 0 (outside the boundary)
yi*f(i) == 1 and 0<alpha< C (on the boundary)
yi*f(i) <= 1 and alpha = C (between the boundary)
'''
if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):
# 如果满足优化的条件,我们就随机选取非i的一个点,进行优化比较
j = selectJrand(i, m)
# 预测j的结果
fXj = float(multiply(alphas, labelMat).T*(dataMatrix*dataMatrix[j, :].T)) + b
Ej = fXj - float(labelMat[j])
alphaIold = alphas[i].copy()
alphaJold = alphas[j].copy()
# L和H用于将alphas[j]调整到0-C之间。如果L==H,就不做任何改变,直接执行continue语句
# labelMat[i] != labelMat[j] 表示异侧,就相减,否则是同侧,就相加。
if (labelMat[i] != labelMat[j]):
L = max(0, alphas[j] - alphas[i])
H = min(C, C + alphas[j] - alphas[i])
else:
L = max(0, alphas[j] + alphas[i] - C)
H = min(C, alphas[j] + alphas[i])
# 如果相同,就没发优化了
if L == H:
print("L==H")
continue
# eta是alphas[j]的最优修改量,如果eta==0,需要退出for循环的当前迭代过程
# 参考《统计学习方法》李航-P125~P128<序列最小最优化算法>
eta = 2.0 * dataMatrix[i, :]*dataMatrix[j, :].T - dataMatrix[i, :]*dataMatrix[i, :].T - dataMatrix[j, :]*dataMatrix[j, :].T
if eta >= 0:
print("eta>=0")
continue
# 计算出一个新的alphas[j]值
alphas[j] -= labelMat[j]*(Ei - Ej)/eta
# 并使用辅助函数,以及L和H对其进行调整
alphas[j] = clipAlpha(alphas[j], H, L)
# 检查alpha[j]是否只是轻微的改变,如果是的话,就退出for循环。
if (abs(alphas[j] - alphaJold) < 0.00001):
print("j not moving enough")
continue
# 然后alphas[i]和alphas[j]同样进行改变,虽然改变的大小一样,但是改变的方向正好相反
alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])
# 在对alpha[i], alpha[j] 进行优化之后,给这两个alpha值设置一个常数b。
# w= Σ[1~n] ai*yi*xi => b = yj- Σ[1~n] ai*yi(xi*xj)
# 所以: b1 - b = (y1-y) - Σ[1~n] yi*(a1-a)*(xi*x1)
# 为什么减2遍? 因为是 减去Σ[1~n],正好2个变量i和j,所以减2遍
b1 = b - Ei- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i, :]*dataMatrix[i, :].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i, :]*dataMatrix[j, :].T
b2 = b - Ej- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i, :]*dataMatrix[j, :].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j, :]*dataMatrix[j, :].T
if (0 < alphas[i]) and (C > alphas[i]):
b = b1
elif (0 < alphas[j]) and (C > alphas[j]):
b = b2
else:
b = (b1 + b2)/2.0
alphaPairsChanged += 1
print("iter: %d i:%d, pairs changed %d" % (iter, i, alphaPairsChanged))
# 在for循环外,检查alpha值是否做了更新,如果在更新则将iter设为0后继续运行程序
# 知道更新完毕后,iter次循环无变化,才推出循环。
if (alphaPairsChanged == 0):
iter += 1
else:
iter = 0
print("iteration number: %d" % iter)
return b, alphas
完整代码地址:SVM简化版,应用简化版SMO算法处理小规模数据集: https://github.com/apachecn/MachineLearning/blob/master/src/python/6.SVM/svm-simple.py
完整代码地址:SVM完整版,使用完整 Platt SMO算法加速优化,优化点:选择alpha的方式不同: https://github.com/apachecn/MachineLearning/blob/master/src/python/6.SVM/svm-complete_Non-Kernel.py
核函数(kernel) 使用
- 对于线性可分的情况,效果明显
- 对于非线性的情况也一样,此时需要用到一种叫
核函数(kernel)的工具将数据转化为分类器易于理解的形式。
利用核函数将数据映射到高维空间
- 使用核函数:可以将数据从某个特征空间到另一个特征空间的映射。(通常情况下:这种映射会将低维特征空间映射到高维空间。)
- 如果觉得特征空间很装逼、很难理解。
- 可以把核函数想象成一个包装器(wrapper)或者是接口(interface),它能将数据从某个很难处理的形式转换成为另一个较容易处理的形式。
- 经过空间转换后:低维需要解决的非线性问题,就变成了高维需要解决的线性问题。
- SVM 优化特别好的地方,在于所有的运算都可以写成内积(inner product: 是指2个向量相乘,得到单个标量 或者 数值);内积替换成核函数的方式被称为
核技巧(kernel trick)或者核"变电"(kernel substation) - 核函数并不仅仅应用于支持向量机,很多其他的机器学习算法也都用到核函数。最流行的核函数:径向基函数(radial basis function)
- 径向基函数的高斯版本,其具体的公式为:
项目案例: 手写数字识别的优化(有核函数)
项目概述
你的老板要求:你写的那个手写识别程序非常好,但是它占用内存太大。顾客无法通过无线的方式下载我们的应用。
所以:我们可以考虑使用支持向量机,保留支持向量就行(knn需要保留所有的向量),就可以获得非常好的效果。
开发流程
收集数据:提供的文本文件
00000000000000001111000000000000
00000000000000011111111000000000
00000000000000011111111100000000
00000000000000011111111110000000
00000000000000011111111110000000
00000000000000111111111100000000
00000000000000111111111100000000
00000000000001111111111100000000
00000000000000111111111100000000
00000000000000111111111100000000
00000000000000111111111000000000
00000000000001111111111000000000
00000000000011111111111000000000
00000000000111111111110000000000
00000000001111111111111000000000
00000001111111111111111000000000
00000011111111111111110000000000
00000111111111111111110000000000
00000111111111111111110000000000
00000001111111111111110000000000
00000001111111011111110000000000
00000000111100011111110000000000
00000000000000011111110000000000
00000000000000011111100000000000
00000000000000111111110000000000
00000000000000011111110000000000
00000000000000011111110000000000
00000000000000011111111000000000
00000000000000011111111000000000
00000000000000011111111000000000
00000000000000000111111110000000
00000000000000000111111100000000
准备数据:基于二值图像构造向量
将 32*32的文本转化为 1*1024的矩阵
def img2vector(filename):
returnVect = zeros((1, 1024))
fr = open(filename)
for i in range(32):
lineStr = fr.readline()
for j in range(32):
returnVect[0, 32 * i + j] = int(lineStr[j])
return returnVect
def loadImages(dirName):
from os import listdir
hwLabels = []
print(dirName)
trainingFileList = listdir(dirName) # load the training set
m = len(trainingFileList)
trainingMat = zeros((m, 1024))
for i in range(m):
fileNameStr = trainingFileList[i]
fileStr = fileNameStr.split('.')[0] # take off .txt
classNumStr = int(fileStr.split('_')[0])
if classNumStr == 9:
hwLabels.append(-1)
else:
hwLabels.append(1)
trainingMat[i, :] = img2vector('%s/%s' % (dirName, fileNameStr))
return trainingMat, hwLabels
分析数据:对图像向量进行目测
训练算法:采用两种不同的核函数,并对径向基核函数采用不同的设置来运行SMO算法
def kernelTrans(X, A, kTup): # calc the kernel or transform data to a higher dimensional space
"""
核转换函数
Args:
X dataMatIn数据集
A dataMatIn数据集的第i行的数据
kTup 核函数的信息
Returns:
"""
m, n = shape(X)
K = mat(zeros((m, 1)))
if kTup[0] == 'lin':
# linear kernel: m*n * n*1 = m*1
K = X * A.T
elif kTup[0] == 'rbf':
for j in range(m):
deltaRow = X[j, :] - A
K[j] = deltaRow * deltaRow.T
# 径向基函数的高斯版本
K = exp(K / (-1 * kTup[1] ** 2)) # divide in NumPy is element-wise not matrix like Matlab
else:
raise NameError('Houston We Have a Problem -- That Kernel is not recognized')
return K
def smoP(dataMatIn, classLabels, C, toler, maxIter, kTup=('lin', 0)):
"""
完整SMO算法外循环,与smoSimple有些类似,但这里的循环退出条件更多一些
Args:
dataMatIn 数据集
classLabels 类别标签
C 松弛变量(常量值),允许有些数据点可以处于分隔面的错误一侧。
控制最大化间隔和保证大部分的函数间隔小于1.0这两个目标的权重。
可以通过调节该参数达到不同的结果。
toler 容错率
maxIter 退出前最大的循环次数
kTup 包含核函数信息的元组
Returns:
b 模型的常量值
alphas 拉格朗日乘子
"""
# 创建一个 optStruct 对象
oS = optStruct(mat(dataMatIn), mat(classLabels).transpose(), C, toler, kTup)
iter = 0
entireSet = True
alphaPairsChanged = 0
# 循环遍历:循环maxIter次 并且 (alphaPairsChanged存在可以改变 or 所有行遍历一遍)
while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
alphaPairsChanged = 0
# 当entireSet=true or 非边界alpha对没有了;就开始寻找 alpha对,然后决定是否要进行else。
if entireSet:
# 在数据集上遍历所有可能的alpha
for i in range(oS.m):
# 是否存在alpha对,存在就+1
alphaPairsChanged += innerL(i, oS)
# print("fullSet, iter: %d i:%d, pairs changed %d" % (iter, i, alphaPairsChanged))
iter += 1
# 对已存在 alpha对,选出非边界的alpha值,进行优化。
else:
# 遍历所有的非边界alpha值,也就是不在边界0或C上的值。
nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
for i in nonBoundIs:
alphaPairsChanged += innerL(i, oS)
# print("non-bound, iter: %d i:%d, pairs changed %d" % (iter, i, alphaPairsChanged))
iter += 1
# 如果找到alpha对,就优化非边界alpha值,否则,就重新进行寻找,如果寻找一遍 遍历所有的行还是没找到,就退出循环。
if entireSet:
entireSet = False # toggle entire set loop
elif (alphaPairsChanged == 0):
entireSet = True
print("iteration number: %d" % iter)
return oS.b, oS.alphas
测试算法:便携一个函数来测试不同的和函数并计算错误率
def testDigits(kTup=('rbf', 10)):
# 1. 导入训练数据
dataArr, labelArr = loadImages('input/6.SVM/trainingDigits')
b, alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, kTup)
datMat = mat(dataArr)
labelMat = mat(labelArr).transpose()
svInd = nonzero(alphas.A > 0)[0]
sVs = datMat[svInd]
labelSV = labelMat[svInd]
# print("there are %d Support Vectors" % shape(sVs)[0])
m, n = shape(datMat)
errorCount = 0
for i in range(m):
kernelEval = kernelTrans(sVs, datMat[i, :], kTup)
# 1*m * m*1 = 1*1 单个预测结果
predict = kernelEval.T * multiply(labelSV, alphas[svInd]) + b
if sign(predict) != sign(labelArr[i]): errorCount += 1
print("the training error rate is: %f" % (float(errorCount) / m))
# 2. 导入测试数据
dataArr, labelArr = loadImages('input/6.SVM/testDigits')
errorCount = 0
datMat = mat(dataArr)
labelMat = mat(labelArr).transpose()
m, n = shape(datMat)
for i in range(m):
kernelEval = kernelTrans(sVs, datMat[i, :], kTup)
# 1*m * m*1 = 1*1 单个预测结果
predict = kernelEval.T * multiply(labelSV, alphas[svInd]) + b
if sign(predict) != sign(labelArr[i]): errorCount += 1
print("the test error rate is: %f" % (float(errorCount) / m))
使用算法:一个图像识别的完整应用还需要一些图像处理的知识,这里并不打算深入介绍
完整代码地址: https://github.com/apachecn/MachineLearning/blob/master/src/python/6.SVM/svm-complete.py
- 作者:片刻 geekidentity
- GitHub地址: https://github.com/apachecn/MachineLearning
- 版权声明:欢迎转载学习 => 请标注信息来源于 ApacheCN